Dans le domaine de la télédétection spatiale les réseaux de neurones sont très souvent utilisés, on les classe dans la catégorie des algorithmes d’intelligence artificielle car ils miment le fonctionnement du cerveau pour acquérir une stratégie de décision d’après l’étude d’une base d’apprentissage.
La comparaison s’arrête là, car il y a encore un gouffre entre la capacité neuronale d’un cerveau et celle d’un algorithme (à mon avis).
Néanmoins, force est de constater qu’ils offrent des possibilités intéressantes pour estimer les variables biophysiques à partir de données de réflectance des satellites Sentinel 2 (A&B)

Le principe est simple, on entraine un réseau de neurones à partir d’une base d’apprentissage issue d’un modèle de réflectance (PROSAIL) qui d’après les données biophysiques d’un couvert végétal calcule un spectre de réflectance, on génère des centaines de milliers de configurations possibles, puis on les soumet au réseau de neurones en inversant le problème: On cherche une ou plusieurs variables biophysiques à partir d’un spectre de réflectance, on parle alors d’inversion de modèle.
L’inversion la plus simple consiste à utiliser un indice de végétation (ex NDVI), ils sont simples à mettre en oeuvre mais insuffisants car ils saturent très vite.
L’intérêt du réseau de neurone est qu’on lui fournit l’ensemble du spectre de réflectance, et que d’après l’apprentissage qu’il a suivi, il va être capable d’interpréter toutes les longueurs d’onde et non pas deux ou trois comme avec un indice. Il crée en quelque sorte son propre indice de végétation qui sera beaucoup plus performant que l’indice NDVI par exemple.
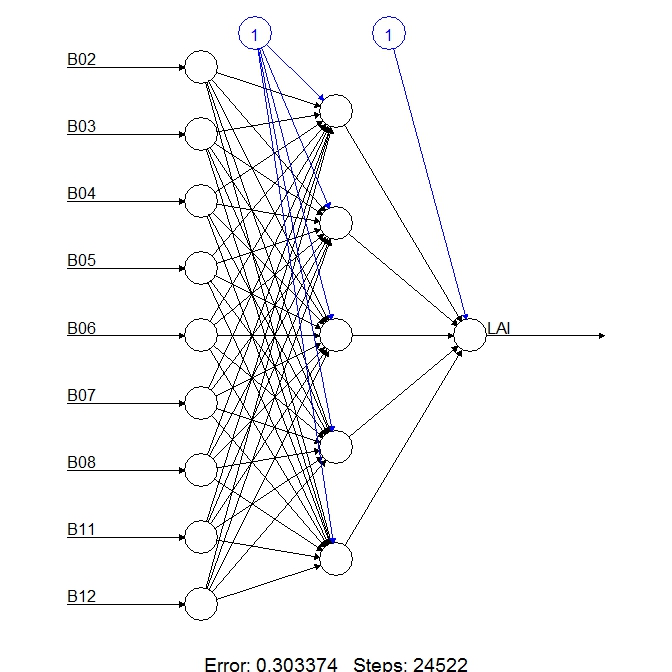
Au jourd’hui, la plupart des chercheurs et utilisateurs de données de télédétection utilisent les réseaux de neurones pour estimer les variables biophysiques comme l’indice foliaire, les indices de végétation sont consacrés à des applications plus simples comme le zonage ou l’estimation du LAI (Indice foliaire) pour des couverts peu denses.
Nénamoins, l’usage des réseaux de neurones exige des calculs lourds et gros consommateurs de mémoire.
Par exemple, pour une tuile Sentinel, on utilise neuf bandes de 10980 pixels de coté, soit 9*120 560 400 cellules dans la matrice de base, c’est à dire 1 085 043 600 pixels (un peu plus d’1 milliard).
J’utilise le logiciel R pour traiter les données Sentinel, sur une machine correcte (2 Proc Xeon et 128 Gigas de mémoire), pour calculer un LAI sur une tuile, il faut 29 minutes en utilisant comme donnée d’entrée les rasters, c’est long !!
En utilisant directement les matrices de données, on réduit ce temps à 447 secondes (c’est mieux !!)
Néanmoins, (j’en suis à cette étape), l’utilisation de code en C++ permet d’aller plus vite, il faut alors programmer toutes les opérations nécessaires comme par exemple le produit de deux matrices comme ceci:
NumericMatrix prodMat(NumericMatrix x,NumericMatrix y,bool linear)
{
int l1=x.nrow();int c1=x.ncol();int c2=y.ncol();
NumericMatrix res(l1,c2);
std::fill(res.begin(),res.end(),0);
int i,j,k;
for(i=0;i<l1;i++){for(j=0;j<c2;j++){for(k=0;k<c1;k++){res(i,j)+=x(i,k)*y(k,j);}
if(!linear) res(i,j)=tanh(res(i,j));}}
return(res);
}
Les puristes diront qu’il existe sans doute des fonctions toutes faites, pas sur, le résultat est converti par la fonction sigmoïde que l’on ne trouve pas dans les méthodes à disposition.
C’est efficace, le temps de calcul est alors réduit à 90 secondes. L’étape suivante sera de tester si la programmation de ces fonctions en parallèle permet encore de réduire le temps de calcul.
Bref, ce genre d’exercice m’a permis de me replonger un peu dans les bouquins de maths sup (poussiéreux) qui trainaient dans ma bibliothèque afin de réviser le calcul matriciel et l’optimisation des matrices denses.